There are different models of machine learning, and an important one is supervised learning 1. This model requires that we have input as well as the corresponding output data. The output data acts as a “supervisor”, comparing the output of the algorithm (i.e. a prediction or Ŷ) to the actual value from data (i.e. Y) in order to calculate the difference between them. This difference (or error) is used to tune the algorithm, and hope that the error is smaller in the next time. Not too different from the first time I learned not to touch a hot surface!
A perceptron is a basic unit of a neural network. It is simply a mathematical function that takes in one or more inputs, performs an operation, and produces an output. The following tutorial goes over the basic functioning of a perceptron.
We can arrange several perceptrons in layers to create a multilayer feedforward neural network. This type of arrangement is a back-propagation network. We call it feedforward because the input propagates sequentially through the layers of the network all the way forward to create an output (i.e. prediction or Ŷ). The prediction is compared to the actual output to calculate an error, which then propagates backwards through the network, tuning weights along the way (hence the back-propagation terminology).
There are a few key equations that give one all the mathematics necessary to create a back-propagation multilayer perceptron network (hereafter referred to as MLP in this post). We will describe these in terms of the forward and backward passes through the network.
The Forward Pass
When a signal propagates forward through an MLP, it creates or induces a field ![]() for the
for the ![]() example of input data at neuron
example of input data at neuron ![]() . This field is computed as:
. This field is computed as:
(1) 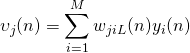
where ![]() is the total amount of incoming connections into neuron
is the total amount of incoming connections into neuron ![]() .
. ![]() is the
is the ![]() input to neuron
input to neuron ![]() , and
, and ![]() is the layer of the network (e.g. for a network with one hidden and an output layer,
is the layer of the network (e.g. for a network with one hidden and an output layer, ![]() will be 1 or 2 respectively). The weight connecting
will be 1 or 2 respectively). The weight connecting ![]() to neuron
to neuron ![]() in layer
in layer ![]() is denoted by
is denoted by ![]() . Note that for the first hidden layer
. Note that for the first hidden layer ![]() is the same as as the
is the same as as the ![]() data input. For other layers, it will represent the output from the respective neurons.
data input. For other layers, it will represent the output from the respective neurons.
Once the induced field is calculated, the output of neuron ![]() can be calculated according to the selected activation function. We will use the hyperbolic tangent function for this purpose2. The output at neuron
can be calculated according to the selected activation function. We will use the hyperbolic tangent function for this purpose2. The output at neuron ![]() is then calculated as:
is then calculated as:
(2) 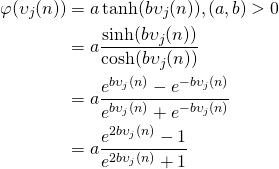
where ![]() ,
, ![]() are constants that are greater than zero. Practically useful values for these constants are
are constants that are greater than zero. Practically useful values for these constants are ![]() and
and ![]() .
. ![]() for neuron
for neuron ![]() and at the
and at the ![]() data example is calculated as in equation 1.
data example is calculated as in equation 1.
And that’s it! Equations 1 & 2 completely specify the forward computational pass through the MLP. Now, let’s look at the more complicated backwards pass.
The Backwards Pass
The first thing we have to do is to compute the error term, ![]() . We can calculate this term by comparing the output at the final neuron in the forward pass. This is the prediction from the neural network for the output for the
. We can calculate this term by comparing the output at the final neuron in the forward pass. This is the prediction from the neural network for the output for the ![]() example of input data, let’s call this
example of input data, let’s call this ![]() . We will compute the error as the difference of this prediction from the actual value,
. We will compute the error as the difference of this prediction from the actual value, ![]() .
.
(3) ![]()
Now, we need the equation to update the weights of the network The equations are not derived here. We use the following equation to update the connecting weights throughout the MLP:
(4) ![]()
where ![]() is the change in the weight connecting neuron
is the change in the weight connecting neuron ![]() in layer
in layer ![]() to neuron
to neuron ![]() in layer
in layer ![]() .
. ![]() is the learning rate constant (the heuristic value for it range from 0.01-5).
is the learning rate constant (the heuristic value for it range from 0.01-5). ![]() is the output of neuron
is the output of neuron ![]() , or in the case of the input layer, it is just the
, or in the case of the input layer, it is just the ![]() input. There is a new term in the equation (4) above, and that is the local gradient function
input. There is a new term in the equation (4) above, and that is the local gradient function ![]() . This function for the output neuron is defined as:
. This function for the output neuron is defined as:
(5) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{align} \delta_j(n) &= \varepsilon_j(n) \varphi'(\upsilon_j(n)), \text{where $j$ is the output neuron} \\ &= \frac{a}{b}[\hat{Y_j}(n) - Y_j(n)][a-Y_j(n)][a+Y_j(n)] \end{align} \end{equation*}](https://predictivemodeler.com/wp-content/ql-cache/quicklatex.com-17c05ce4d66d0470daa17002fc0b23a0_l3.png)
where ![]() and
and ![]() are the same constants as from equation (2),
are the same constants as from equation (2), ![]() is the first order differential of equation (2).
is the first order differential of equation (2).
Now that you have the local gradient for the output neuron from (5), you can use equation (4) to update the weights of the incoming connections to the output neuron. In order to update the connecting weights to any hidden neurons, you need to first calculate the local gradient at each of the hidden neurons using the following equation:
(6) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{align} \delta_j(n) &= \varphi'(\upsilon_j(n))\sum_k \delta_k(n) w_{kj}(n), \text{where $j$ is a hidden neuron} \\ &= \frac{a}{b}[a-Y_j(n)][a+Y_j(n)]\sum_k \delta_k(n) w_{kj}(n) \end{align} \end{equation*}](https://predictivemodeler.com/wp-content/ql-cache/quicklatex.com-d0e4f45e5a32ce7344375fdd75b65db9_l3.png)
where ![]() is over all of the outgoing connectors connecting neuron
is over all of the outgoing connectors connecting neuron ![]() in layer
in layer ![]() to neuron
to neuron ![]() in layer
in layer ![]() .
.
Using equation (6) and equation (4), you can now update the remaining weights in the neural network.
I know that was a lot of algebra! Fear not – in the next post I will provide a simple working model of this mathematics in Microsoft Excel. You will be able to see the workings of the forward and backwards pass in live action!


3 thoughts on “Theory: The Multi-Layer Perceptron”
I have added a third hidden neuro to your Excel model. Would like to send the file to you. Do you have an address to send the Excel file?
Ron
davis
Thank you for the work Ron! You may send it to syed@predictivemodeler.com.
Please send me a copy